海量数据处理

分治

对于海量数据，无法一次性装进内存处理，通过hash映射分割成相应的小块数据，然后对各个小块数据操作

例 1 ：a、b文件中相同的 url

给定a、b两个文件，各存放50亿个 url , 每个 url 各占64字节，内存限制是 4GB ,找出a、b文件中相同的 url ？
5*64=320GB

方法1：

1. 遍历a,对每个url求取hash（url）%1024 , 1024个小文件，每个大约300MB;
2. 遍历b,1024
3. 处理后，相同的url都在对应的小文件，（a0vsb0,a1vsb1……a1024vsb1024）,不对应的小文件不可能有相同的url处理后，相同的url都在对应的小文件
4. a存入hasf_set,遍历b

方法2：
如果允许有一定的错误率，可以使用Bloom filter，4G内存大概可以表示340亿bit。将其中一个文件中的 url 使用Bloom filter映射为这340亿bit，然后挨个读取另外一个文件的url，检查是否与Bloom filter，如果是，那么该url应该是共同的 url （注意会有一定的错误率）

例 2 ：访问最多的IP

海量日志数据，提取出某日访问百度次数最多的那个IP
方法：
百度作为国内第一大搜索引擎，每天访问它的IP数量巨大，如果想一次性把所有IP数据装进内存处理，则内存容量明显不够，故针对数据太大，内存受限的情况，可以把大文转化成（取模映射）小文件，从而大而化小，逐个处理

1. 分而治之/hash映射
   首先把这一天访问百度日志的所有IP提取出来，然后逐个写入到一个大文件中，接着采用映射的方法，比如%1000，把整个大文件映射为1000个小文件。

2. hash_map统计
   当大文件转化成了小文件，那么我们便可以采用 hash_map(ip, value) 来分别对1000个小文件中的IP进行频率统计，再找出每个小文件中出现频率最大的IP。

3. 堆/快速排序
   统计出1000个频率最大的IP后，依据各自频率的大小进行排序(可采取堆排序)，找出那个频率最大的IP，即为所求。

例 3 ：Top K 问题

有一个1G大小的一个文件，里面每一行是一个词，词的大小不超过16字节，内存限制大小是1M。返回频数最高的100个词

方法：

1. 分而治之/hash映射
   顺序读取文件，对于每个词x，取hash(x)%5000，然后把该值存到5000个小文件（记为x0,x1,…x4999）中，每个文件大概是200k。如果其中有的小文件超过了1M大小，按照类似的方法继续往下分，直到分解得到的小文件的大小都不超过1M。

2. hash_map统计
   对每个小文件，采用trie树/hash_map等统计每个文件中出现的词以及相应的频率。

3. 堆/归并排序
   取出出现频率最大的100个词（可以用含100个结点的最小堆）后，再把100个词及相应的频率存入文件，这样又得到了5000个文件。最后把这5000个文件进行归并（类似于归并排序）。

Bit-map

使用位数组来表示某些元素是否存在

由于采用了Bit为单位来存储数据，因此在存储空间方面，可以大大节省，故适用于海量数据的快速查找、判重、删除

示例：
对0-7内的5个元素(4,7,2,5,3)排序（假设元素没有重复），相应位置 1

遍历一遍Bit区域，将该位是一的位的编号输出（2，3，4，5，7），就达到了排序的目的

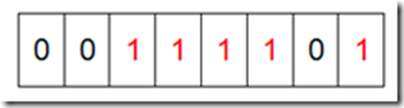
例 1：不重复的整数

在2.5亿个整数中找出不重复的整数（内存不足以容纳这2.5亿个整数）

解法一：

采用2-Bitmap（每个数分配2bit，00表示不存在，01表示出现一次，10表示多次，11无意义）进行，共需内存2^32 * 2 bit=1 GB内存（因为整数最多有2^32个）。然后扫描这2.5亿个整数，查看Bitmap中相对应位，如果是00变01，01变10，10保持不变。所描完事后，查看bitmap，把对应位是01的整数输出即可。

解法二：
进行划分小文件的方法。然后在小文件中找出不重复的整数，并排序。然后再进行归并，注意去除重复的元素。”

例 2 ：快速判断

给40亿个不重复的unsigned int的整数，没排过序的，然后再给一个数，如何快速判断这个数是否在那40亿个数当中？

方法：
申请 2^32 = 512M的内存，一个bit位代表一个unsigned int值。读入40亿个数，设置相应的bit位，读入要查询的数，查看相应bit位是否为1，为1表示存在，为0表示不存在。

Bloom Filter

如果想判断一个元素是不是在一个集合里，一般是将集合中所有元素保存起来，然后通过比较确定。应用链表、树、哈希表 等数据结构

但是随着集合中元素的增加，需要的存储空间越来越大、同时检索速度也越来越慢
以上三种时间复杂度分别为 O(n),O(log n),O(n/k)

Bit-map 的升级版
适用于需要进一步节省内存、但可允许一定错误率的情况

原理

当一个元素被加入集合时，通过K个散列函数将这个元素映射成一个位数组中的K个点，把它们置为1。

检索时，只要看这些点是不是都是1就（大约）知道集合中有没有它：如果这些点有任何一个0，则被检元素一定不在；如果都是1，则被检元素很可能在。

初始状态时，Bloom Filter 是一个包含m位的位数组，每一位都置为0。

为了表达 S = { x1, x2,…,xn } 这样一个n个元素的集合，Bloom Filter使用k个相互独立的哈希函数，分别将集合中的每个元素映射到{1,…,m}的范围中。对任意一个元素x，第i个哈希函数映射的位置hi(x)就会被置为1（1≤i≤k）。

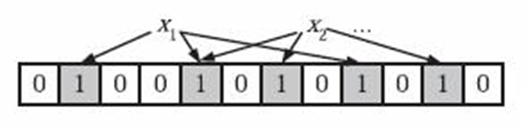
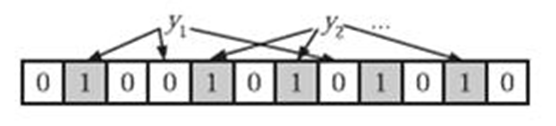
在判断y是否属于这个集合时，我们对y应用k次哈希函数，如果所有hi(y)的位置都是1（1≤i≤k），那么我们就认为y是集合中的元素，否则就认为y不是集合中的元素。

下图中 y1 就不是集合中的元素（因为y1有一处指向了“0”位）。
y2属于这个集合，或者刚好是一个false positive。

Trie （字典）树

典型应用： 统计和排序大量的字符串，搜索引擎系统用于文本词频统计，代码补全，统计具有相同首部的字符串

优点： 最大限度地减少无谓的字符串比较，查询效率比较高。

核心思想： 空间换时间，利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。

三个基本性质：

1. 根节点不包含字符，除根节点外每一个节点都只包含一个字符。
2. 从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串。
3. 每个节点的所有子节点包含的字符都不相同。

例 1 ：单词查询判断

假如现在给你10万个长度不超过10的单词，对于每一个单词，我们要判断它出没出现过，如果出现了，求第一次出现在第几个位置。

方法：
假设要查询的单词是abcd，只要找以a开头的单词中是否存在abcd就可以了，同样的，在以a开头中的单词中，只考虑以b作为第二个字母的单词

即如果有b，abc，abd，bcd，abcd，efg，hii 6个单词，可以构建一棵树：

对于每一个节点，从根遍历到他的过程就是一个单词，如果这个节点被标记为红色，就表示这个单词存在，否则不存在。
对于一个单词，只要顺着从根走到对应的节点，再看这个节点是否被标记为红色就可以知道它是否出现过了。把这个节点标记为红色，就相当于插入了这个单词。

这样一来我们查询和插入可以一起完成，所用时间仅仅为单词长度（在这个例子中，便是10）。这就是一棵trie树。
可以看到，trie树每一层的节点数是26^i级别的。所以为了节省空间，我们还可以用动态链表，或者用数组来模拟动态。而空间的花费，不会超过单词数×单词长度。

例 2 ：最频繁出现的前10个词

一个文本文件，大约有一万行，每行一个词，要求统计出其中最频繁出现的前10个词，请给出思想，给出时间复杂度分析

方法

用trie树统计每个词出现的次数，时间复杂度是O(n*len)（len表示单词的平均长度），然后是找出出现最频繁的前10个词。当然，也可以用堆来实现，时间复杂度是O(nlg10)。所以总的时间复杂度，是O(nle)与O(nlg10)中较大的哪一个。

倒排索引

原理

倒排索引是一种索引方法，被用来存储在全文搜索下某个单词在一个文档或者一组文档中的存储位置的映射，常被应用于搜索引擎、关键字查询、学术论文的关键字搜索的问题中。

要被索引的文本

要被索引的文本

正向索引用来存储每个文档的单词的列表。正向索引的查询往往满足每个文档有序频繁的全文查询和每个单词在校验文档中的验证这样的查询。在正向索引中，文档占据了中心的位置，每个文档指向了一个它所包含的索引项的序列。

也就是说正向索引文档指向了它包含的那些单词，而反向索引则是单词指向了包含它的文档。

外排序

原理

顾名思义，即在内存外面的排序，因为当要处理的数据量很大，而不能一次装入内存时，此时只能放在读写较慢的外存储器（硬盘）上。

外排序通常采用的是一种“排序-归并”的策略。

1. 在排序阶段，先读入能放在内存中的数据量，将其排序输出到一个临时文件，依次进行，将待排序数据组织为多个有序的临时文件；

2. 尔后在归并阶段将这些临时文件组合为一个大的有序文件，也即排序结果。

例1 ：给10^7个数据量的磁盘文件排序

输入：给定一个文件，里面最多含有n个不重复的正整数（也就是说可能含有少于n个不重复正整数），且其中每个数都小于等于n，n=10^7。
输出：得到按从小到大升序排列的包含所有输入的整数的列表。
条件：最多有大约1MB的内存空间可用，但磁盘空间足够。且要求运行时间在5分钟以下，10秒为最佳结果。

分析

1. 输入数据限制在相对较小的范围内，
2. 数据没有重复，
3. 其中的每条记录都是单一的整数，没有任何其它与之关联的数据。

方法1：位图

第一次，只处理1—4999999之间的数据，这些数都是小于5000000的，对这些数进行位图排序，只需要约5000000/8=625000Byte，也就是0.625M，排序后输出。

第二次，扫描输入文件时，只处理4999999-10000000的数据项，也只需要0.625M（可以使用第一次处理申请的内存）。
用此位图方法，严格说来还是不太行，空间消耗10^7 / 8 还是大于1M（1M=1024*1024空间，小于10^7/8）。

用位图方案的话，需要约1.25MB（若每条记录是8位的正整数的话，则10000000/(102410248) ~= 1.2M）的空间，

方法2：多路归并

1. 内部排序
   可用内存为1MB，每次对250K的数据进行排序，然后将有序的数写入硬盘。10M的数据需要循环40次，最终产生40个有序的文件。

2. 归并排序（可使用败者树 ）
   将每个文件最开始的数读入，存放在大小为40的 数组中；
   选择数组中最小的数 min_data，及其对应的文件索引index；
   将数组中最小的数写入文件result，然后更新数组 (根据index读取该文件下一个数代替min_data)；

败者树
log(n)的时间内找到最值

算法的步骤是：每次从k个组中的首元素中选一个最小的数，加入到新组，这样每次都要比较k-1次，故
算法复杂度为O((n-1)(k-1))，而如果使用败者树，可以在O(logk)的复杂度下得到最小的数，算法复杂
度将为O((n-1)logk)， 对于外部排序这种数据量超大的排序来说，这是一个不小的提高。